Αριθμητικός-γεωμετρικός μέσος (όρος)

Στα μαθηματικά, ο αριθμητικός-γεωμετρικός μέσος (όρος) (AGM ή agM) δύο θετικών πραγματικών αριθμών x και y είναι το αμοιβαίο όριο μιας ακολουθίας αριθμητικών μέσων και μιας ακολουθίας γεωμετρικών μέσων. Ο αριθμητικός-γεωμετρικός μέσος χρησιμοποιείται σε γρήγορους αλγορίθμους για εκθετικές, τριγωνομετρικές και άλλες ειδικές συναρτήσεις, καθώς και για ορισμένες μαθηματικές σταθερές, ιδίως για τον υπολογισμό του π.

Διάγραμμα του αριθμητικού-γεωμετρικού μέσου $\operatorname {agm} (1,x)$ μεταξύ διαφόρων γενικευμένων μέσων.

Ο AGM ορίζεται ως το όριο των αλληλοεξαρτώμενων ακολουθιών $a_{i}$ και $g_{i}$: ${\begin{aligned}a_{0}&=x,\\g_{0}&=y\\a_{n+1}&={\tfrac {1}{2}}(a_{n}+g_{n}),\\g_{n+1}&={\sqrt {a_{n}g_{n}}}\,.\end{aligned}}$

Αυτές οι δύο ακολουθίες συγκλίνουν στον ίδιο αριθμό, τον αριθμητικό-γεωμετρικό μέσο όρο των x και y- συμβολίζεται με M'(x, y), ή μερικές φορές με agm(x, y) ή AGM(x, y).

Ο αριθμητικός-γεωμετρικός μέσος μπορεί να επεκταθεί σε μιγαδικούς αριθμούς και όταν οι κλάδοι της τετραγωνικής ρίζας μπορούν να ληφθούν ασυνεπώς, είναι γενικά μια συνάρτηση πολλαπλών τιμών .

Παράδειγμα

Για να βρεθεί ο αριθμητικός-γεωμετρικός μέσος του

${\begin{array}{rcccl}a_{1}&=&{\tfrac {1}{2}}(24+6)&=&15\\g_{1}&=&{\sqrt {24\cdot 6}}&=&12\\a_{2}&=&{\tfrac {1}{2}}(15+12)&=&13.5\\g_{2}&=&{\sqrt {15\cdot 12}}&=&13.416\ 407\ 8649\dots \\&&\vdots &&\end{array}}$

Οι πρώτες πέντε επαναλήψεις δίνουν τις ακόλουθες τιμές:

n	an	gn
0	24	6
1	15	12
2	13.5	13.416 407 864 998 738 178 455 042...
3	13.458 203 932 499 369 089 227 521...	13.458 139 030 990 984 877 207 090...
4	13.458 171 481 7 45 176 983 217 305...	13.458 171 481 7 06 053 858 316 334...
5	13.458 171 481 725 615 420 766 8 20...	13.458 171 481 725 615 420 766 8 06...

Ο αριθμός των ψηφίων στα οποία το a_n και το g_n συμφωνούν (υπογραμμισμένο) περίπου διπλασιάζεται με κάθε επανάληψη. Ο αριθμητικός-γεωμετρικός μέσος των 24 και 6 είναι το κοινό όριο αυτών των δύο ακολουθιών, το οποίο είναι περίπου 13.4581714817256154207668131569743992430538388544.

Ιστορία

Ο πρώτος αλγόριθμος που βασίστηκε σε αυτό το ζεύγος ακολουθιών εμφανίστηκε στα έργα του Λαγκράνζ. Οι ιδιότητές του αναλύθηκαν περαιτέρω από τον Γκάους.

Ιδιότητες

Ο γεωμετρικός μέσος δύο θετικών αριθμών δεν είναι ποτέ μεγαλύτερος από τον αριθμητικό μέσο. Επομένως, ο (g_n) είναι μια αύξουσα ακολουθία, ο (a_n) είναι μια φθίνουσα ακολουθία και ο g_n ≤ M(x, y) ≤ a_n. Αυτές είναι αυστηρές ανισότητες x ≠ y.

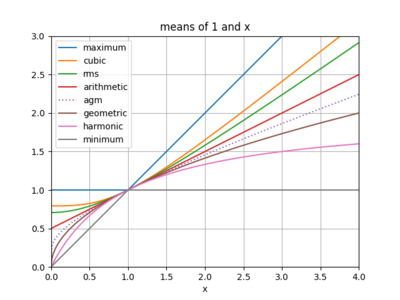
M(x, y) είναι επομένως ένας αριθμός μεταξύ του γεωμετρικού και του αριθμητικού μέσου των x και y; είναι επίσης μεταξύ των x και y.

Αν r ≥ 0, τότε M(rx,ry) = r M(x,y).

Υπάρχει μια έκφραση ολοκληρωτικής μορφής για την M(x,y):

${\begin{aligned}M(x,y)&={\frac {\pi }{2}}\left(\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\sqrt {x^{2}\cos ^{2}\theta +y^{2}\sin ^{2}\theta }}}\right)^{-1}\\&=\pi \left(\int _{0}^{\infty }{\frac {dt}{\sqrt {t(t+x^{2})(t+y^{2})}}}\right)^{-1}\\&={\frac {\pi }{4}}\cdot {\frac {x+y}{K\left({\frac {x-y}{x+y}}\right)}}\end{aligned}}$

όπου K(k) είναι το πλήρες ελλειπτικό ολοκλήρωμα πρώτου είδους:

$K(k)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\sqrt {1-k^{2}\sin ^{2}(\theta )}}}$

Δεδομένου ότι η αριθμητική-γεωμετρική διαδικασία συγκλίνει τόσο γρήγορα, παρέχει έναν αποτελεσματικό τρόπο υπολογισμού ελλειπτικών ολοκληρωμάτων, τα οποία χρησιμοποιούνται, για παράδειγμα, στο σχεδιασμό ελλειπτικών φίλτρων.

Ο αριθμητικός-γεωμετρικός μέσος συνδέεται με τη συνάρτηση θ 3 του Ιακόμπι $\theta _{3}$ με

$M(1,x)=\theta _{3}^{-2}\left(\exp \left(-\pi {\frac {M(1,x)}{M\left(1,{\sqrt {1-x^{2}}}\right)}}\right)\right)=\left(\sum _{n\in \mathbb {Z} }\exp \left(-n^{2}\pi {\frac {M(1,x)}{M\left(1,{\sqrt {1-x^{2}}}\right)}}\right)\right)^{-2},$

που, όταν $x=1/{\sqrt {2}}$ δίνει

$M(1,1/{\sqrt {2}})=\left(\sum _{n\in \mathbb {Z} }e^{-n^{2}\pi }\right)^{-2}.$

Σχετικές έννοιες

Το αντίστροφο του αριθμητικού-γεωμετρικού μέσου του 1 και της τετραγωνικής ρίζας του 2 είναι η σταθερά του Γκάους.

${\frac {1}{M(1,{\sqrt {2}})}}=G=0.8346268\dots$

Το 1799, ο Γκάους απέδειξε Μέχρι το 1799, ο Γκάους είχε δύο αποδείξεις του θεωρήματος, αλλά καμία από αυτές δεν ήταν αυστηρή από τη σύγχρονη άποψη. ότι

$M(1,{\sqrt {2}})={\frac {\pi }{\varpi }}$

όπου $\varpi$ είναι η σταθερά του Λημνισκάτ.

Το 1941, το $M(1,{\sqrt {2}})$ (και συνεπώς το $G$) αποδείχθηκε υπερβατικό από τον Θεόδωρο Σνάιντερ. Το σύνολο $\{\pi ,M(1,1/{\sqrt {2}})\}$ είναι αλγεβρικά ανεξάρτητο πάνω στο $\mathbb {Q}$, αλλά το σύνολο $\{\pi ,M(1,1/{\sqrt {2}}),M'(1,1/{\sqrt {2}})\}$ (όπου ο πρώτος αριθμός δηλώνει την παράγωγο ως προς τη δεύτερη μεταβλητή) δεν είναι αλγεβρικά ανεξάρτητη στο $\mathbb {Q}$. Στην πραγματικότητα,

$\pi =2{\sqrt {2}}{\frac {M^{3}(1,1/{\sqrt {2}})}{M'(1,1/{\sqrt {2}})}}.$

Ο γεωμετρικός-αρμονικός μέσος GH μπορεί να υπολογιστεί χρησιμοποιώντας ανάλογες ακολουθίες γεωμετρικών και αρμονικών μέσων, και μάλιστα GH(x,y) = 1/M(1/x, 1/y) = xy/M(x,y). Ο αριθμητικός-αρμονικός μέσος όρος είναι ισοδύναμος με τον γεωμετρικό μέσο όρο.

Ο αριθμητικός-γεωμετρικός μέσος μπορεί να χρησιμοποιηθεί - μεταξύ άλλων - για τον υπολογισμό λογαρίθμων, πλήρων και ατελών ελλειπτικών ολοκληρωμάτων πρώτου και δεύτερου είδους και ελλειπτικών συναρτήσεων Ιακόμπι.

Απόδειξη της ύπαρξης

Η ανισότητα των αριθμητικών και γεωμετρικών μέσων συνεπάγεται ότι

$g_{n}\leq a_{n}$

και ως εκ τούτου

$g_{n+1}={\sqrt {g_{n}\cdot a_{n}}}\geq {\sqrt {g_{n}\cdot g_{n}}}=g_{n}$

Δηλαδή, η ακολουθία g_n είναι μη φθίνουσα και οριοθετείται παραπάνω από το μεγαλύτερο των x και y. Σύμφωνα με το θεώρημα μονοτονικής σύγκλισης, η ακολουθία είναι συγκλίνουσα, οπότε υπάρχει ένα g τέτοιο ώστε:

$\lim _{n\to \infty }g_{n}=g$

Ωστόσο, μπορούμε επίσης να διαπιστώσουμε ότι:

$a_{n}={\frac {g_{n+1}^{2}}{g_{n}}}$

και κατά συνέπεια:

$\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }{\frac {g_{n+1}^{2}}{g_{n}}}={\frac {g^{2}}{g}}=g$

Q.E.D.

Απόδειξη της έκφρασης με ολοκληρωτική μορφή

Η απόδειξη αυτή δίνεται από τον Γκάους. Έστω

$I(x,y)=\int _{0}^{\pi /2}{\frac {d\theta }{\sqrt {x^{2}\cos ^{2}\theta +y^{2}\sin ^{2}\theta }}},$

Αλλαγή της μεταβλητής ολοκλήρωσης σε $\theta '$, όπου

$\sin \theta ={\frac {2x\sin \theta '}{(x+y)+(x-y)\sin ^{2}\theta '}},$

$\cos \theta ={\frac {\sqrt {(x+y)^{2}-2(x^{2}+y^{2})\sin ^{2}\theta '+(x-y)^{2}\sin ^{4}\theta '}}{(x+y)+(x-y)\sin ^{2}\theta '}},$

$\cos \theta \ d\theta =2x{\frac {(x+y)-(x-y)\sin ^{2}\theta '}{((x+y)+(x-y)\sin ^{2}\theta ')^{2}}}\ \cos \theta 'd\theta '\ ,$

$d\theta ={\frac {2x\cos \theta '((x+y)-(x-y)\sin ^{2}\theta ')}{((x+y)+(x-y)\sin ^{2}\theta '){\sqrt {(x+y)^{2}-2(x^{2}+y^{2})\sin ^{2}\theta '+(x-y)^{2}\sin ^{4}\theta '}}}}d\theta '\ ,$

$$x^{2}\cos ^{2}\theta +y^{2}\sin ^{2}\theta ={\frac {x^{2}((x+y)^{2}-2(x^{2}+y^{2})\sin ^{2}\theta '+(x-y)^{2}\sin ^{4}\theta ')+4x^{2}y^{2}\sin ^{2}\theta '}{((x+y)+(x-y)\sin ^{2}\theta ')^{2}}}={\frac {x^{2}((x+y)-(x-y)\sin ^{2}\theta ')^{2}}{((x+y)+(x-y)\sin ^{2}\theta ')^{2}}}$$

Έτσι προκύπτει

$${\frac {d\theta }{\sqrt {x^{2}\cos ^{2}\theta +y^{2}\sin ^{2}\theta }}}={\frac {2x\cos \theta '((x+y)-(x-y)\sin ^{2}\theta ')}{((x+y)+(x-y)\sin ^{2}\theta '){\sqrt {(x+y)^{2}-2(x^{2}+y^{2})\sin ^{2}\theta '+(x-y)^{2}\sin ^{4}\theta '}}}}{\frac {((x+y)+(x-y)\sin ^{2}\theta ')}{x((x+y)-(x-y)\sin ^{2}\theta ')}}={\frac {2\cos \theta 'd\theta '}{\sqrt {(x+y)^{2}-2(x^{2}+y^{2})\sin ^{2}\theta '+(x-y)^{2}\sin ^{4}\theta '}}},$$

δίνει

${\begin{aligned}I(x,y)&=\int _{0}^{\pi /2}{\frac {d\theta '}{\sqrt {{\bigl (}{\frac {1}{2}}(x+y){\bigr )}^{2}\cos ^{2}\theta '+{\bigl (}{\sqrt {xy}}{\bigr )}^{2}\sin ^{2}\theta '}}}\\&=I{\bigl (}{\tfrac {1}{2}}(x+y),{\sqrt {xy}}{\bigr )}.\end{aligned}}$

Συνεπώς, έχουμε

${\begin{aligned}I(x,y)&=I(a_{1},g_{1})=I(a_{2},g_{2})=\cdots \\&=I{\bigl (}M(x,y),M(x,y){\bigr )}=\pi /{\bigr (}2M(x,y){\bigl )}.\end{aligned}}$

Η τελευταία ισότητα προκύπτει από την παρατήρηση ότι $I(z,z)=\pi /(2z)$.

Τέλος, προκύπτει το επιθυμητό αποτέλεσμα

$M(x,y)=\pi /{\bigl (}2I(x,y){\bigr )}.$

Εφαρμογές

Ο αριθμός π

Σύμφωνα με τον αλγόριθμο Γκάους-Λεζάντρ,

$\pi ={\frac {4\,M(1,1/{\sqrt {2}})^{2}}{1-\displaystyle \sum _{j=1}^{\infty }2^{j+1}c_{j}^{2}}},$

όπου

$c_{j}={\frac {1}{2}}\left(a_{j-1}-g_{j-1}\right),$

με $a_{0}=1$ και $g_{0}=1/{\sqrt {2}}$, τα οποία μπορούν να υπολογιστούν χωρίς απώλεια ακρίβειας χρησιμοποιώντας

$c_{j}={\frac {c_{j-1}^{2}}{4a_{j}}}.$

Πλήρες ελλειπτικό ολοκλήρωμα K(sinα)

Με $a_{0}=1$ και $g_{0}=\cos \alpha$ προκύπτει το AGM

$M(1,\cos \alpha )={\frac {\pi }{2K(\sin \alpha )}},$

όπου K'(k) είναι ένα πλήρες ελλειπτικό ολοκλήρωμα πρώτου είδους:

$K(k)=\int _{0}^{\pi /2}(1-k^{2}\sin ^{2}\theta )^{-1/2}\,d\theta .$

Με άλλα λόγια, αυτό το τέταρτο περιόδου μπορεί να υπολογιστεί αποτελεσματικά με τη χρήση του AGM,

$K(k)={\frac {\pi }{2M(1,{\sqrt {1-k^{2}}})}}.$

Άλλες εφαρμογές

Χρήση αυτής της ιδιότητας του AGM μαζί με τους ανοδικούς μετασχηματισμούς του Τζον Λάντεν, Ρίτσαρντ Π. Μπρεντ πρότειναν τους πρώτους αλγορίθμους AGM για τη γρήγορη αξιολόγηση στοιχειωδών υπερβατικών συναρτήσεων (e^x, cos x, sin x). Στη συνέχεια, πολλοί συγγραφείς συνέχισαν να μελετούν τη χρήση των αλγορίθμων AGM.

Δημοσιεύσεις

• E. T. Whittaker, G. N. Watson - A Course of Modern eClass ΕΚΠΑ
• Pi - Unleashed

Δείτε επίσης

• David H. Bailey et al. The Quest for Pi (PDF)

Εξωτερικοί σύνδεσμοι

• English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
• Jonathan M. Borwein, Peter B. Borwein: Pi and the AGM, A Study in Analytic Number Theory and Computational Complexity. John Wiley, New York 1987, ISBN 0-471-31515-X.
• Louis Vessot King: On the direct numerical calculation of elliptic functions and integrals. Cambridge University Press, 1924,
• Tom M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Second Edition (1990), Springer, New York ISBN 0-387-97127-0