Άρρητος αριθμός

Άρρητος αριθμός ονομάζεται κάθε αριθμός ο οποίος δεν είναι δυνατό να εκφραστεί ως ανάγωγο κλάσμα ${\frac {\mu }{\nu }}$, όπου $\mu$ και $\nu$ είναι ακέραιοι αριθμοί, με $\nu$ διάφορο του μηδενός, σε αντίθεση με τους ρητούς αριθμούς, οι οποίοι μπορούν να εκφραστούν ως ανάγωγο κλάσμα ακεραίων.

Ο αριθμός $\scriptstyle {\sqrt {2}}$ είναι άρρητος

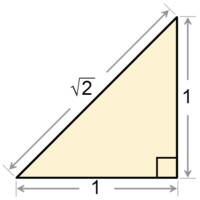
Παραδείγματα άρρητων αριθμών είναι το π ή το e και η τετραγωνική ρίζα του 2 ($\scriptstyle {\sqrt {2}}$).

Οι άρρητοι αριθμοί είναι όλοι οι πραγματικοί αριθμοί (R) οι οποίοι δεν είναι ρητοί. Ως εκ τούτου και ελλείψει μοναδικού συμβολισμού για το σύνολο των αρρήτων, χρησιμοποιείται ο έμμεσος συμβολισμός I (Irrational numbers) ή $\mathbb {Q} ^{c}$ ή $\mathbb {R} \setminus \mathbb {Q}$, όπου $\mathbb {R}$ το σύνολο των πραγματικών αριθμών και $\mathbb {Q}$ το σύνολο των ρητών. Οι άρρητοι αριθμοί έχουν άπειρο αριθμό, μη επαναλαμβανόμενων περιοδικά, δεκαδικών ψηφίων.

Μία χαρακτηριστική ιδιότητα των άρρητων αριθμών είναι ότι το άθροισμα δύο άρρητων δίνουν μερικές φορές

ως αποτέλεσμα έναν ρητό αριθμό. Για παράδειγμα 0,101001000100001000001...+1,0101101110111101111101111110...=1,11111111111....=${\frac {10}{9}}$

Ιστορικό

Η πρώτη καταγραφή για τη γνώση των άρρητων αριθμών ξεκινά με τον Ίππασο, έναν πυθαγόρειο που είτε αποκάλυψε πως η διαγώνιος ενός τετραγώνου με πλευρά ακέραιο δεν είναι ακέραιος ή ανακάλυψε τους άρρητους στην προσπάθεια να αναγνωρίσει τις πλευρές του πενταγράμμου. Οι Πυθαγόρειοι δίδασκαν ότι οποιοσδήποτε φυσικός αριθμός μπορεί να εκφραστεί ως λόγος δυο άλλων φυσικών αριθμών και διέδιδαν πως με τη χρήση των αριθμών μπορούσαν να επιλύσουν όλα τα προβλήματα του πραγματικού κόσμου. Η πρώτη ενδεχομένως κρίση στα Μαθηματικά εμφανίστηκε συνοδευόμενη από πολιτική κρίση όταν, σύμφωνα με την παράδοση, ο Ίππασος ο Μεταπόντιος (450 π.Χ.) αποκάλυψε τον άρρητο, γεγονός που φύλαγαν μυστικό οι Πυθαγόρειοι, και προκάλεσε την εξέγερση των λαών που τελούσαν υπό την εξουσία των Πυθαγορείων.

Περαιτέρω ανάγνωση

Ελληνικά άρθρα

• «Άρρητοι (ασύμμετροι) αριθμοί». Ευκλείδης Β΄ (1): 26-30. 1978. http://www.hms.gr/apothema/?s=sa&i=3552. 
• «Αναστήλωση των Γεωμετρικών Αποδείξεων του Θεοδώρου του Κυρηναίου για το Ασύμμετρο των Ριζών του 3, 5,... 17». Ευκλείδης Β΄ (1): 17-20. 1989. http://www.hms.gr/apothema/?s=sa&i=2850. 

Ξενόγλωσσα άρθρα

• Jourdain, Philip E. B. (Ιανουαρίου 1908). «The Introduction of Irrational Numbers». The Mathematical Gazette 4 (69): 201–209. doi:10.2307/3602961. https://archive.org/details/sim_mathematical-gazette_1908-01_4_69/page/201. 
• Heath, A.C. (Μαΐου 1927). «On the Approximation to Irrational Numbers By Rationals». The Mathematical Gazette 13 (188): 362–366. doi:10.2307/3603106. https://archive.org/details/sim_mathematical-gazette_1927-05_13_188/page/362. 
• Chari, V. T. (Δεκεμβρίου 1944). «1768. Irrational numbers». The Mathematical Gazette 28 (282): 197–197. doi:10.2307/3609571. https://archive.org/details/sim_mathematical-gazette_1944-12_28_282/page/197. 
• Goodstein, R. L. (Δεκεμβρίου 1941). «Recurring Digits in Irrational Decimals». The Mathematical Gazette 25 (267): 273–278. doi:10.2307/3606555. https://archive.org/details/sim_mathematical-gazette_1941-12_25_267/page/273. 
• Lord, Nick (Νοεμβρίου 2008). «92.75 Maths bite: irrational powers of irrational numbers can be rational». The Mathematical Gazette 92 (525): 534–534. doi:10.1017/S0025557200183846. https://archive.org/details/sim_mathematical-gazette_2008-11_92_525/page/534. 
• Zhou, Li (Νοεμβρίου 2011). «Irrationality proofs à la Hermite». The Mathematical Gazette 95 (534): 407–413. doi:10.1017/S0025557200003491. https://archive.org/details/sim_mathematical-gazette_2011-11_95_534/page/407. 

Δείτε επίσης

• Αριθμός
• Ρητός αριθμός

Εξωτερικοί σύνδεσμοι

• Πολυμέσα σχετικά με το θέμα Irrational numbers στο Wikimedia Commons