Παράδοξο του Κράμερ

Στα μαθηματικά, το παράδοξο του Κράμερ ή το παράδοξο των Κράμερ-Όιλερ είναι ο ισχυρισμός ότι ο αριθμός των σημείων τομής δύο καμπυλών ανώτερης τάξης στο επίπεδο μπορεί να είναι μεγαλύτερος από τον αριθμό των αυθαίρετων σημείων που συνήθως απαιτούνται για τον ορισμό μιας από αυτές τις καμπύλες. Πήρε το όνομά του από τον Γενεάτη μαθηματικό Γκαμπριέλ Κράμερ.

Οι εννέα τομές των $x^{3}-x=10(y^{3}-y)$ και $y^{3}-y=10(x^{3}-x)$

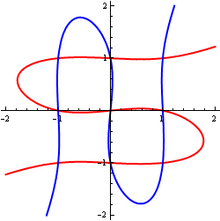
Το φαινόμενο αυτό φαίνεται παράδοξο, επειδή τα σημεία τομής δεν ορίζουν με μοναδικό τρόπο καμία καμπύλη (ανήκουν σε τουλάχιστον δύο διαφορετικές καμπύλες) παρά τον μεγάλο αριθμό τους. Προκύπτει από μια αφελή κατανόηση ή λανθασμένη εφαρμογή δύο θεωρημάτων:

• Το θεώρημα του Μπεζούτ ισχυρίζεται ότι ο αριθμός των σημείων τομής δύο αλγεβρικών καμπυλών είναι ίσος με το γινόμενο των βαθμών τους, αν πληρούνται ορισμένες αναγκαίες συνθήκες. Συγκεκριμένα, δύο καμπύλες βαθμού $n$ έχουν γενικά $n^{2}$ σημεία τομής.
• Το θεώρημα του Κράμερ υποδηλώνει ότι μια καμπύλη βαθμού $n^{2}$ προσδιορίζεται από $n(n+3)/2$ σημεία, πάντα με την προϋπόθεση ότι πληρούνται ορισμένες προϋποθέσεις.

Για όλα τα $n\geq 3$, $n^{2}\geq n(n+3)/2$, οπότε θα φαινόταν αφελώς ότι για βαθμό τρία ή μεγαλύτερο, η τομή δύο καμπυλών θα είχε αρκετά σημεία για να ορίσει μία από τις καμπύλες μοναδικά. Ωστόσο, επειδή τα σημεία αυτά ανήκουν και στις δύο καμπύλες, δεν ορίζουν μια μοναδική καμπύλη αυτού του βαθμού. Η επίλυση του παράδοξου είναι ότι το όριο $n(n+3)/2$ για τον αριθμό των σημείων που απαιτούνται για τον ορισμό μιας καμπύλης ισχύει μόνο για σημεία σε γενική θέση. Σε ορισμένες εκφυλισμένες περιπτώσεις, $n(n+3)/2$ σημεία δεν είναι αρκετά για να καθορίσουν μια καμπύλη με μοναδικό τρόπο.

Ιστορία

Το παράδοξο δημοσιεύθηκε για πρώτη φορά από τον Κόλιν Μακλάουριν το 1720. Ο Κράμερ και ο Λέοναρντ Όιλερ αλληλογραφούσαν για το παράδοξο σε επιστολές του 1744 και 1745 και ο Όιλερ εξήγησε το πρόβλημα στον Κράμερ. Έγινε γνωστό ως το παράδοξο του Κράμερ αφού εμφανίστηκε στο βιβλίο του 1750 Εισαγωγή στην Ανάλυση των Αλγεβρικών Καμπύλων Γραμμών, αν και ο Κράμερ ανέφερε τον Μακλάουριν ως πηγή της δήλωσης. Περίπου την ίδια εποχή, ο Όιλερ δημοσίευσε παραδείγματα που έδειχναν μια κυβική καμπύλη που δεν οριζόταν μοναδικά από 9 σημεία[. και συζήτησε το πρόβλημα στο βιβλίο του Introductio in analysin infinitorum. Το αποτέλεσμα δημοσιοποιήθηκε από τον Τζέιμς Στίρλινγκ και διευκρινίστηκε από τον Γιούλιους Πλούκερ.

Κανένα παράδοξο για ευθείες γραμμές και μη εκφυλισμένες κωνικές

Για καμπύλες πρώτης τάξης (δηλαδή Ευθείες), το παράδοξο δεν εμφανίζεται, επειδή $n=1$, οπότε $n^{2}=1<n(n+3)/2=2$. Γενικά, δύο διαφορετικές ευθείες τέμνονται σε ένα σημείο, εκτός αν έχουν την ίδια κλίση, οπότε δεν τέμνονται καθόλου. Ένα μόνο σημείο δεν είναι αρκετό για να οριστεί μια ευθεία (χρειάζονται δύο)- το σημείο τομής διέρχεται όχι μόνο από τις δύο δεδομένες ευθείες, αλλά και από έναν άπειρο αριθμό άλλων ευθειών.

Δύο μη εκφυλισμένες κωνικές τέμνονται το πολύ σε τέσσερα πεπερασμένα σημεία στο πραγματικό επίπεδο, που είναι ακριβώς ο αριθμός που δίνεται ως μέγιστος από το θεώρημα του Μπεζού. Ωστόσο, απαιτούνται πέντε σημεία για να οριστεί μια μη εκφυλισμένη κωνική, οπότε δεν υπάρχει παράδοξο σε αυτή την περίπτωση.

Το παράδειγμα του Κράμερ για κυβικές καμπύλες

Το παράδειγμα του Κράμερ με εκφυλισμένες κυβικές καμπύλες x³ − x = 0 (μπλε) και y³ − y = 0 (κόκκινο)

Σε επιστολή του προς τον Όιλερ, ο Κράμερ επισήμανε ότι οι κυβικές καμπύλες $x^{3}-x=0$ και $y^{3}-y=0$ τέμνονται σε ακριβώς εννέα σημεία. Η πρώτη εξίσωση ορίζει τρεις κατακόρυφες ευθείες $x=-1$, $x=0$, και $x=1$, και ομοίως η δεύτερη εξίσωση ορίζει τρεις οριζόντιες ευθείες- οι ευθείες αυτές τέμνονται σε ένα πλέγμα εννέα σημείων. Επομένως, εννέα σημεία δεν αρκούν για τον μοναδικό προσδιορισμό μιας κυβικής καμπύλης σε εκφυλισμένες περιπτώσεις όπως αυτές.

Λύση κατά τον Όιλερ

Μια εξίσωση σε δύο μεταβλητές βαθμού n έχει 1 + n(n + 3) / 2 συντελεστές, αλλά το σύνολο των σημείων που περιγράφονται από την εξίσωση διατηρείται αν η εξίσωση διαιρεθεί με έναν από τους μη μηδενικούς συντελεστές, αφήνοντας έναν συντελεστή ίσο με 1 και μόνο n(n + 3) / 2 συντελεστές για να χαρακτηρίσουν την καμπύλη. Δεδομένου n(n + 3) / 2 σημείων (x_i, y_i), κάθε ένα από αυτά τα σημεία μπορεί να χρησιμοποιηθεί για τη δημιουργία μιας ξεχωριστής εξίσωσης αντικαθιστώντας το στη γενική πολυωνυμική εξίσωση βαθμού n, δίνοντας n(n + 3) / 2 γραμμικές εξισώσεις στους άγνωστους n(n + 3) / 2 συντελεστές. Εάν αυτό το σύστημα είναι μη εκφυλισμένο με την έννοια ότι έχει μη μηδενικό προσδιοριστή, οι άγνωστοι συντελεστές προσδιορίζονται μοναδικά και έτσι η πολυωνυμική εξίσωση και η καμπύλη της προσδιορίζονται μοναδικά. Αν όμως ο προσδιοριστής είναι μηδέν, το σύστημα είναι εκφυλισμένο και τα σημεία μπορεί να βρίσκονται σε περισσότερες από μία καμπύλες βαθμού n.

Εξωτερικοί σύνδεσμοι

• Ed Sandifer "Cramer’s Paradox"
• Cramer's Paradox at MathPages
• Robert E. Bradley & Lee Stemkoski "When Nine Points Are Worth But Eight: Euler’s Resolution of Cramer’s Paradox – Euler's Letter to Cramer"

Βιβλιογραφία

• A Source Book in Mathematics, 1200-1800
• History of Analytic Geometry
• "The Collected Mathematical Papers, Τόμος 1"
• "How Euler Did Even More I"